Der mehrdimensionale Fermat

Vor kurzem wurde die Welt der Mathematik in helle Aufregung versetzt. Der japanische Mathematiker Shinichi Mochizuki erklärte in einem über 100 Seiten starken Dokument, dass er eine Lösung für das alte Problem der abc-Vermutung der Primzahlen habe.

Da aus jener Vermutung auch der Große Fermatsche Satz (eine ehemalige Vermutung) entspringt, wäre es somit ein weiterer Beweis für dessen Vermutung.

Nun gibt es schon einen Beweis von Andrew Wiles, aber der Ansatz der abc-Vermutung scheint einfacher und weniger komplex zu sein.

Leider hält sich die Mathematik mit der die abc-Vermutung weiterhin in der einfachen Dimension auf, während es eine andere Vermutung gibt, die viele Unlogik der eindimensionalen Vermutungen erklären könnte – wenn man sie beweisen sollte. Wir haben schon darüber berichtet und wollen es an dieser Stelle erneut darlegen.

Kaum ein Mathematiker oder Physiker kommt daran vorbei: Die Fermat Vermutung. Seit dem Beweis 1994 auch Fermats letzter Satz genannt. Über 300 Jahre kämpften gelehrte Mathematiker und Hobby- Zahlentheoretiker um den Beweis oder um den Gegenbeweis.

Köpfe von Rang und Namen bissen sich die Zähne aus. Bis der englische Mathematiker Andrew Wiles 1994 ansatzweise und dann 1995 mit seinem ehemaligen Schüler Richard Taylor zweifelsfrei die Richtigkeit des Satzes beweisen konnte.

Die Quintessenz des Beweises wäre aber, dass man keine ganzzahligen Würfel miteinander addieren könnte um so einen ganzzahligen Würfel zu erhalten. Wie kommt dieses Ergebnis zustande? Auf der Reise durch die mathematische Welt der Zahlentheoretiker gelangten wir dabei zu einer erstaunlichen Erkenntnis und einer neuen Vermutung. In diesem Beitrag wollen wir diese Reise kurz skizzieren.

Alles begann mit dem Satz von Pythagoras, den Pierre de Fermat in Aufzeichnungen fand.

.

.

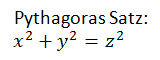
Jedem Schüler ist dieser Satz durchaus bekannt. Interessanterweise lässt sich daraus berechnen, wie zwei Quadrate miteinander addiert und zu einem größeren Quadrat zusammengefügt werden. Hier sind vor allem jene Quadrate interessant, bei denen nur ganzzahlige Werte im Spiel sind. Als Beispiel gilt nach wie vor die kleinste ganzzahlige Lösung mit x=3, y=4 und z=5.

.

.

.

Fermats Gedanken gingen an dieser Stelle wahrscheinlich aus Langeweile weiter. Er berechnete Ergebnisse für den Fall 3 als Potenz.

.

.

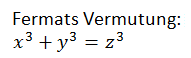
Für das obige Beispiel zeigte sich, dass die kleinste ganzzahlige Lösung des Pythagoras Satz nicht gilt.

.

.

.

Fermat ging sogar soweit, dass er die Vermutung aufstellte, dass es für alle Potenzen größer als 2 keine ganzzahligen Lösungen geben würde. Bis heute ist es keinem Menschen gelungen, eine solche zu finden.

.

.

.

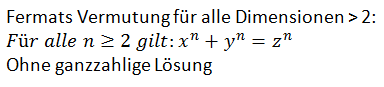
An dieser Stelle reizte er die Nachwelt der Mathematiker mit einer schriftlichen Randnotiz in einem Buch, das der einzige überlieferte Gedankengang Fermats für seine Beweisführung bleiben sollte:

„Es ist unmöglich, einen Kubus in zwei Kuben zu zerlegen, oder ein Biquadrat in zwei Biquadrate, oder allgemein irgendeine Potenz größer als die zweite in Potenzen gleichen Grades. Ich habe hierfür einen wahrhaft wunderbaren Beweis gefunden, doch ist der Rand hier zu schmal, um ihn zu fassen.“

Fast 360 Jahre quälte dieser Satz die Nachwelt, Mathematiker der Welt suchten nach dem Beweis. Am Ende fanden ihn Andrew Wiles und sein ehemaliger Student Richard Taylor. Für den eigentlichen Beweis reicht an dieser Stelle der Platz nicht aus. Nur so viel: Es waren viele vorherigen Irrtümer und viele später folgende mathematischen Errungenschaften notwendig, um den Beweis zu erbringen.

Beim Nachdenken nach einer möglichen Lösung, um ganzzahlige Würfel nun doch einfach addieren zu können gerieten wir auf eine ähnliche Reise wie einst Fermat: Fermat erhöhte einfach die Potenz der Pythagoras Satz. Was aber passiert, wenn man nun auch ein weiteres Element in die Formulierung bringt?

.

Wie schon Fermat gegenüber Pythagoras haben wir uns gegenüber Fermat erlaubt, den Satz um eine Note zu verändern. Wir nennen sie die Lösung im dreidimensionalen Raum. Denn wir bringen einer einst für den zweidimensionalen Raum mit x und y im rechtwinkligem Dreieck erdachten Formulierung eine dritte Komponente analog zu Länge, Breite und Höhe hinzu. Es wäre analog ein dreidimensionales rechtwinkliges Dreieck. Interessant ist, dass man sofort eine Fortsetzung der ganzzahligen Pythagoras Lösung wiederfindet:

.

.

.

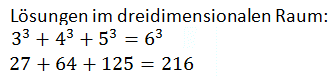
Um es analog mit Fermats Worten zu sagen:

„Es ist in der Tat möglich, einen Kubus in drei Kuben zu zerlegen, oder ein Biquadrat in drei Biquadrate, oder allgemein irgendeine Potenz größer als die zweite in Potenzen gleichen Grades.“

Wir möchten also so weit gehen, dass es für jede Dimension mindestens eine entsprechende ganzzahlige Lösung gibt.

.

.

.

.

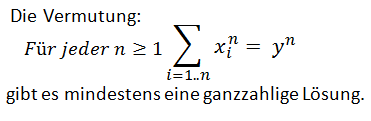
Wie Fermat wollen wir an dieser Stelle den Beweis vorerst schuldig bleiben. Denn es ist nur eine Skizze auf dieser neuen Reise, die wir fortsetzen wollen.

Michael Starke, München.

.